Slot spel matematiker
Nya casino webbplatser för att spela med riktiga pengar
De flesta bord spel satsningar betalas i en "X-till-1" mode. Vad detta betyder är att om spelaren vinner omgången, hans insats är tillbaka och han är utbetalas ett tilläggsbelopp för sin seger. Om spelaren förlorar, då hans insats är bort från bordet. Vissa satsningar på tabellen spel är mycket liknande till slots. Till exempel pair plus satsning i tre korts poker har en rak pay table bygger på tre kort delas ut till spelaren. Det brukar betalar 1-till-1" för ett par, "3-till-1" för en flush, "6-till-1" för en stege, "30-till-1" för resor och "40-till-1" för en straight flush. Denna sida satsning kunde lika väl vara en slot, eftersom det kräver inte en strategi, men det har ganska konstiga betala tabell: "2, 4, 7, 31, 41."
DET ULTIMATA GAMING MATEMATIK GUIDE
Möjlighet att spela casino spel är en produkt som konsumenten köper med sina spel dollar. Den ståndpunkt som jag tar är att spelaren vill ha en viss erfarenhet när han sitter på ett spel och är villiga att betala för den upplevelsen med hjälp av den oundvikliga bita huset kanten tar.
För att fullt ut förstå den produkt spelaren inköp kräver en resa i matematik av casino spel. Marknadsföring måste förstå detta material när de utvecklar effektiva strategier. Varje del av en spelare interaktion med en casino spel har sin egen matematik. Satsningar har "odds" som avgör hur mycket du vill betala spelare om han vinner. Den andel av tiden vinner spelaren som kallas "hit frekvens." den "house edge" är den andel av spelarens totala inledande satsningar på att huset räknar med att hålla på lång sikt om spelaren använder en perfekt strategi. Den "theo" eller "teoretiska" är det faktiska beloppet casino förväntar sig att vinna från spelaren. "Return to player" åtgärder som den andel av spelarens totala satsningar spelaren betalas tillbaka i live casino-spela.
X-1, X-1, 1-I-X
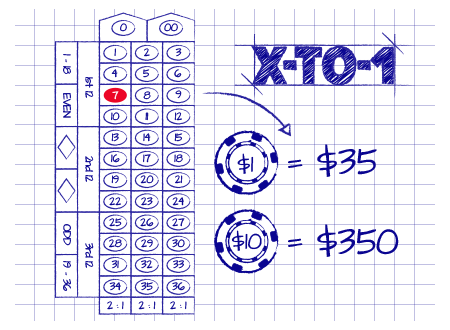
De flesta bord spel satsningar betalas i en "X-till-1" mode. Vad detta betyder är att om spelaren vinner omgången, hans insats är tillbaka och han är utbetalas ett tilläggsbelopp för sin seger. Om spelaren förlorar, då hans insats är bort från bordet.
Till exempel, om en spelare satsar på rött-7 rakt upp i roulette då utdelningen är 35-till-1. Om hans insats är $10, då han antingen vinner $350 (35 × $10) och hans $10 är tillbaka, eller som han förlorar $10.
Denna typ av ersättning är olika från spelautomater. För slots, varje gång spelaren trycker på knappen eller drar i handtaget, ett belopp som dras av från hans kredit balans. Det är hans insats. Då hjulen snurra, och när de slutar han är betalat ett belopp som baseras på de mönster som visas av hjulen genom att hänvisa till några utdelnings tabell. Oavsett vad resultatet av hjulen, spelarens ursprungliga satsning är förverkad. Vi säger att slots är "X-för-1."

De flesta satsningar på keno, lotterier, slots och video poker betalas "X-för-1." denna förvirring har använts på ett effektivt sätt, till exempel i blackjack spelautomater. Blackjack slots visar vanligtvis en utbetalning på 2 poäng när spelare får en blackjack. Den spelare känner att blackjack är vanligtvis betalar 3-till-2, så det verkar vara en söt affär. Detta är dock utbetalningen är 2-för-1. Därmed spelaren förlorar sin ursprungliga 1 kredit-och då vinner tillbaka 2 poäng om han får en blackjack. Spelaren nät 1 kredit på detta sätt. Därmed 2-för-1 är samma som 1-till-1. Några skulle spela bordet spelet av blackjack om utbetalningen för en blackjack var reducerade till 1-till-1, men folk ofta spelar dessa slots med en utbetalning på 2-för-1.
Den progressiva satsning i caribbean stud är ett exempel på ett "X 1" satsning som förekommer i ett väl kända för bordsspel. Spelarens insats går automatiskt in när det är gjort, och ett ljus tänds på bordet som visar den spelare som har gjort denna satsning. Ett annat vanligt "X 1" satsning är bad-beat jackpot i poker rummet. Potten bidrar $1 vardera hand till den progressiva; att pengar förlorar.
Det är vanligt att satsningar betalar ut "X-till-1" på en bord spel, exempel på framgångsrika "X-för-1 satsningar på bordsspel är sällsynta (ett exempel är den hop satsningar i craps). Tillbaka spelarens ursprungliga satsning om du vinner eller tryck, på annat sätt samla spelarens satsning. Bordsspel och slots är olika djur och den mest grundläggande skillnaden är att slots betala "X-för-1."
Vissa satsningar på tabellen spel är mycket liknande till slots. Till exempel pair plus satsning i tre korts poker har en rak pay table bygger på tre kort delas ut till spelaren. Det brukar betalar 1-till-1" för ett par, "3-till-1" för en flush, "6-till-1" för en stege, "30-till-1" för resor och "40-till-1" för en straight flush. Denna sida satsning kunde lika väl vara en slot, eftersom det kräver inte en strategi, men det har ganska konstiga betala tabell: "2, 4, 7, 31, 41."
Slutligen, den terminologi som "1-i-X" är vanligt förekommande, men inte i samband med utbetalningar. Till exempel, i craps, kallas det att shooter får en 7 (på lång sikt) 1-i-6 rullar. I dubbel-0 roulette, antalet röda-7 kommer upp (på lång sikt) 1: 38 spins. Spelaren får blackjack (på lång sikt) cirka 1-i-den 21 händerna. Den terminologi som "1-i-X" har ingenting att göra med hur mycket ett spel betalar en vinnande satsning. Det används för att beskriva graden av förekomst av en händelse vid ett bord spel.
Slot spel matematiker





|
Alla spel maskiner är konstruerade för att betala spelare tillbaka en del av vad spelas. Beloppen varierar från maskin till maskin och från casino till casino. Alla maskiner har en sak gemensamt: ju längre tid maskinen är spelade, ju närmare den faktiska utbetalningar kommer att vara att de teoretiska resultaten.
Slot maskiner använder ett slumpmässigt urval process för att uppnå en uppsättning teoretiska odds. Slumpmässigt urval innebär att varje gång spaken dras och hjulen sätts i rörelse av en kombination av symboler är slumpmässigt utvalda. Den "slumpmässiga" aspect garanterar att varje dra i handtaget är oberoende från alla andra dra, så att resultaten av den föregående dra, och den innan det, har ingen effekt på den nuvarande.
Den teoretiska odds är inbyggd i konstruktion och program i maskinen, och det är möjligt att beräkna den exakta utbetalningsprocent för varje maskin på lång sikt.
Med undantag för den video slots, spelautomater har hjul som kallas rullar med symboler tryckta på varje hjul. Varje rulle symbol representerar ett stopp som kan komma att vila på payline, och kan eller inte kan vara en del av en kombination av symboler resulterar i en payoff.
Sannolikheten för att vinna någon utdelning på varje slot maskin är relaterade till antalet rullar och antalet symboler på varje hjul.
Den vanligaste typen av mekaniska slot maskinen har tre rullar med tjugo-symboler på varje hjul. För att beräkna det totala antalet kombinationer av symboler på denna maskin, vi flera antalet stopp (symboler) på varje rulle med antalet stannar på var och en av de återstående hjulen. För en tre hjuls maskinen med tjugo stationer per rulle, vi har 20 x 20 x 20 = 8000 kombinationer av slot symboler.
Om en jackpot som erbjuds på den här maskinen betalar den 7 7 7 och bara en 7-symbol på varje rulle, då sannolikheten för att träffa denna jackpot är 1/20 x 1/20 x 1/20 eller en på 8 000. Om två 7-symboler på en rulle, då vår beräkning är 2/20 x 1/20 x 1/20 för en sannolikhet 1/4,000 för att träffa jackpotten.
På samma sätt kan vi beräkna sannolikheten för varje kombination av symboler för att slå om vi vet hur många gånger varje symbol visas på varje rulle.
När mekaniska slots dominerade, var det inte alltför svårt att räkna de symboler på varje hjul och bestämma exakt payoff för en viss maskin. Med mikroprocessor kontrollerad slots denna uppgift har blivit nästan omöjligt, eftersom antalet stopp per rulle kan vara så många som 256. För att fastställa utdelningen av en sådan maskin skulle kräva betydande reverse engineering och är utanför omfånget för nästan alla spelare.
Hur många hjul har en större effekt på sannolikheter än det antal symboler per rulle. Om vi jämför en maskin med 32 stationer per hjul och 3 rullar, med en 22-stopp per rulle maskinen och 4 hjulen, kommer du att se den enorma skillnaden annan rulle gör:
32 stop, 3 hjul: 32 x 32 x 32 = 32,768 kombinationer
22 stoppa, 4 rulle: 22 x 22 x 22 x 22 = 234,256 kombinationer
Om vi betraktar en 5-hjuls maskin med 32 stationer per rulle, finner vi över 33 miljoner kombinationer!
Varje maskin har en förutbestämd utbetalningsprocent. När du hör saker som "våra slots betala tillbaka till 98,3%", detta betyder att på lång sikt för varje dollar som sitter i maskinen, kommer den att återgå till 98,3 cent. Omvänt, kan vi konstatera att för varje dollar som spelas, kasino kommer att behålla 1,7 cent. Dessa procentsatser endast att gälla under mycket lång sikt spela som består av hundratusentals eller miljontals spelar.
Många människor misstolkar dessa procentsatser och tror att om de spelar med $100.00 på 98.3% återbetalning maskinen att de bara kan förlora $1.70. Det finns ett par saker som är fel med denna tankegång. För det första, teoretiska procenttal kommer att uppnås endast under långa perioder av att spela. Över ett par dussin, eller ens ett par hundra rullar, avkastning procent kommer att variera kraftigt. För det andra, om en person tar $100.00 för slot spela, han eller hon vanligtvis inte kommer att begränsa hans eller hennes pjäs att sätta in detta belopp av pengar i maskinen endast en gång. De flesta människor kommer att köpa tjugo dollar värt av polletter och fortsätta att spela med dessa pengar tills det är borta. Efter insättning av den första omgången av mynt i maskinen, de kommer att fortsätta spela med några mynt kvar i facket, och de kommer att fortsätta med detta mönster tills inga mynt kvar. Och sedan undrar de över hur det var möjligt för en till 98,3% slot att ta alla sina pengar.
Svaret är att kasinot fortsätter att extrahera dess andel på varje mynt sätts in i maskinen. Den spelare som inte kommer att begränsa hans spel till tjugo dollar eller hundra dollar men kommer att fortsätta att pågående mynt. Maskinen kommer att, åtminstone på lång sikt, fortsätter att slipa bort alla pengar spelas.
Tabell 6 visar de förödande effekt på huset kanten kan ha på spelarens spelkonto. Denna tabell jämförs slot håll procentsatser av från två procent till femton procent för tio omgångar av spel, från och med $100.
Tabell 6. Belopp per spelomgång
Slot spel matematiker
I dag, matematik av slot maskiner. University of houston matematik institutionen presenterar här programmet om maskiner för att göra vår civilisation köra, och människor vars uppfinningsrikedom skapade dem.
M athematicians först blev intresserad av slumpmässighet genom att studera hasardspel. Allt sedan dess historia av matematik och spel har varit sammanflätade. Smart spelare använda matematik för att leta efter den minsta fördelar och kasinon använda avancerade matematiska verktyg för att ta fram nya sätt att rita spelarna.
Ja, ett patent som har beviljats till den norska matematikern inge telnaes 1984 omvandlas spelindustrin. Innan telnaes' uppfinning, spelautomater var i huvudsak mekaniska anordningar. Förutom att vara svårt att ställa in och underhålla, mekaniska slot maskiner drabbats av ett viktigt problem: låt oss titta på en maskin med tre hjul, vart och ett med 12 symboler, med en av de 12 symboler ett körsbär. Sannolikheten för att få tre körsbär, och att vinna jackpotten är 1 på 1,728. Om casino vill tjäna pengar, jackpotten ska vara, säger $1,700 på en 1 $satsning. Det verkar inte som attraktiva av dagens standarder. Men det enda sättet att öka utbetalningen är att minska chanserna att träffa en jackpot.
Lägga till en annan rulle är en möjlighet. Till exempel att lägga till en fjärde rulle i det föregående exemplet skulle få oss att vinna jackpotten på ca $20,000. Men folk gillar inte maskiner med fler hjul — de intuitivt, och med rätta, känner att extra hjulen minskar deras chans att vinna. En annan möjlighet är att sätta fler symboler på varje hjul. Men den astronomiska jackpots som du ser i kasinon i dag skulle då kräva verkligen enorma maskiner.
Inge telnaes föreslog en enkel lösning: låt en random number generator — ett datorchip — fastställa den kombination av symboler som visas när hjulen stannar. Med andra ord, använda ett chip att kontrollera när hjulen sluta på en dragning, men skapar en illusion av att hjulen slutat på egen hand. Antalet möjliga utfall på spelautomaten inte ändras. Men, genom att programmera chip, operatören har full kontroll över sannolikheten för de olika utfallen. Till exempel operatören som skulle göra tre körsbär visas bara en gång i en miljon spins.
Detta var en lysande inblick: antag att jag väljer ett nummer mellan ett och en miljon. Skulle du vara villig att satsa på att du kan gissa att antalet? Svaret är: förmodligen inte. Men låt en dator chip plocka ett sådant nummer, placera marker i maskinen med blinkande lampor och snurrande hjul, och många människor kommer att vara mer än villiga att göra en insats. Det beror helt enkelt på vad människor antar är det som händer i en spelmaskin är mycket olika från vad som faktiskt händer.
Magikern oljemålning av hieronymus boschfrån mellan 1475 och 1480
Historia av spel är också sammanflätade med en mindre ansedd grupp — bluffmakare och bedragare. I det långa loppet, det enda säkra sättet att tjäna pengar genom spel är att skapa en illusion av att dina motståndare kan vinna, samtidigt som oddsen fast på din sida. Och som ger dem som vet att matte en mycket solid fördel.
Jag är kreљimir josić, vid university of houston, där vi är intresserade av hur uppfinningsrika sinnen arbete.
(tema musik)
OBSERVERA: i exemplet med tre körsbär, jag antog att man bara vinner i de fall spin resultat i tre körsbär, och det är ingen annan vinnande kombination. I verkligheten finns det vanligtvis många vinnande kombination, och som ett resultat, jackpot skulle vara ännu mindre.
Följande berättelse i wired magazine visar nackdelarna av den nya generationens spelautomater — de är lättare att hacka och att counterfit än deras mekaniska motsvarighet http://www.Wired.Com/magazine/2011/07/ff_scammingslots/.
Här är en mer uttömmande diskussion om historien av slot maskiner och slumpmässiga nummer generatorer inom dem http://catlin.Casinocitytimes.Com/article/non-random-randomness-part-1-1243. Kanske du vill bläddra mot slutet av artikeln för att läsa om hur brister i utformningen av spel maskin resulterat i någon plocka 19 av de 20 vinnande nummer i ett spel på KENO — och gjorde det 3 gånger i rad. Som person gick bort med $620,000, men bara efter några kontroverser.
Båda bilderna är från wikipedia. Spelautomaten bilden togs av jeff kubina.
För mer matematik i vardagen, besök kjosic.Wordpress.Com.
Denna episod var först sändes den 7 september, 2011
Slot spel matematiker
Vill du arbeta i en fartfylld och dynamiskt företag som ligger i framkant av online gaming?
Arbeta tillsammans med design-och utvecklingsteam, spelmaskin matematiker kommer att vara ansvarig för att skapa och verifiera matematik modeller för online spelautomater.
Huvudsakliga ansvarsområden
Vinnaren kommer att vara bekväm att producera matematiska modeller av spelautomater i excel och producerar simuleringar i java, och kommer antingen har ett starkt intresse eller en vilja att lära sig om spelautomater.
De matematiska modeller som är centrala för att lyckas i en spelmaskin, och matematikern kommer att spela en central roll i att utveckla nya spel begrepp och mekanik.
Tidsgränserna är snäva och andra avdelningar beror på leverans i tid för matematik modeller och simuleringar, så det är viktigt att kandidaten kan uppskatta det arbete som krävs för att med rimlig noggrannhet och uppfyller överenskomna tidsfrister.
Stark skriftlig engelska är viktigt i denna roll för att säkerställa komplexa idéer kommuniceras tydligt.
Detta är en 100% distansjobba jobb, ingen flytt krävs.
Kompetens som krävs
• matematik – för högskoleexamen med en viss inriktning på sannolikhetsteori.
• kunskap på hög nivå programmeringsspråk såsom C++, python, java, ruby, C#
• kunskap om bästa kodning metoder, förmåga att skriva rent underhålla koden
• erfarenhet inom matematisk modellering, statistisk analys och djup förståelse för finansiell riskhantering
• excel
• kreativt tänkande
• förmåga att organisera tid och arbete för att snäva deadlines
• god analytisk förmåga
• engelska
Önskad kompetens
• erfarenhet av att producera matematiska modeller för spel program
• intresse och/eller erfarenhet av spelautomater
• inlägg examen i matematik eller naturvetenskap examen
Slots matematik
Slots är mycket populära i både landbaserade och online kasinon. De erbjuder spelare ett brett utbud av spännande möjligheter att vinna, med den progressiva jackpotten som det yttersta målet. Som en spelare fortsätter att spela slots spel, han/hon kan komma över en mängd olika sätt för att vinna, såsom normala vinster, scatter-vinster, innehar och knuffar, free spins, spelar och bonus spel. I var och en av dessa det är ett komplext system av slots matematik på spela – och dina chanser att vinna varierar avsevärt beroende på vilket skede av spelet är aktiverad. Till exempel, i ett bonusspel där du står en mycket bättre chans att vinna än i vanligt spel.
När vi hänvisar till "chansen att vinna" vi drar starkt på teorin om sannolikhet, som är en viktig del av spelandet matematik. För att räkna ut sannolikheten för att en viss vinst på en slots maskin, ska du först använda combin funcion för att beräkna antalet sätt som finns för att bilda en viss kombination, och sedan dividera den siffran med antalet sätt som finns för att bilda alla möjliga kombinationer på hjulen. Till exempel, om du räknat ut att det finns 250 sätt att få en viss kombination, och att det finns en summa av 250 000 möjliga kombinationer att en viss slots spelet kan återvända, då sannolikheten för att din valda kombinationen kommer upp är 250/250 000 = 0.1%.
Den utbetalningsprocent på spelautomater
Den utbetalningsprocent på slot maskiner är programmerade till sina elektroniskt-programmable read-only memory (EPROM), och dessa siffror kan endast ändras med vederbörligt tillstånd och godkännande från relevanta spel myndigheterna i ett visst land/region. Den korrekta förfaranden som måste följas för att ändra värdena för online spelautomater. Slot-maskiner har normalt en utbetalningsprocent på mellan 85% och 98%, beroende på kasinot och den typ av maskin. Den genomsnittliga hus fördel för slots spel har beräknats till cirka 9% av märket.
Skalning returer
Slot-maskiner i de flesta landbaserade kasinon fungerar på ett system för skalning avkastning; det är, det är mer värt mödan att spela högre valörer, som utbetalningsprocent på dessa maskiner tenderar att vara högre än för den lägre valör maskiner. Med andra ord, högre valör maskiner har ett mindre hus kanten än den lägre valör maskiner. Men, online-kasinon tenderar att hålla sitt hus kanter – och därmed vinstutdelningsprocent – konsekvent över alla valörer.
Läs om casino spel matematik populära spel, eller ta en titt på gambling matematik ordlista.
Slot spel matematiker
Konfigurationer
det finns ett brett utbud av spelautomater med beaktande av parametrisk design och regler. Konfiguration av en slot maskin är angivna med konfiguration av displayen och konfigurationen av hjulen.
Visning av slot maskinen visar resultat av hjulen i grupper av fläckar (plats hänvisar till en enhet som en del av en rulle som håller en symbolen synlig genom dess fönster; en plats på displayen motsvarar en sluta av rullen; ett fönster kan innehålla en eller flera platser) som har en viss form och arrangemang. Konfiguration av displayen kan definieras och modelleras matematiskt genom ett kartesiskt rutnät av heltal, där grid's poäng står för hjul fläckar/stopp och (ersätta) - line är en ändlig mängd av minst 3 poäng som kan anslutas via en väg som förbinder successivt närliggande intressanta att ställa. Längden på en rad är kardinalitet av att ställa. De flesta spelautomater har displayen ordnas som ett rektangulärt rutnät. Linjer kan ha vilken form som helst och komplexitet, och det har alla typer av geometriska och topologiska egenskaper. Det är horisontella, vertikala, sned, eller brutna linjer; symmetrisk, tvärgående linjer; trekantiga, trapetsformade, sicksack, trappa, eller dubbel-trappa linjer.
Fördelningen och utformningen av de symboler på varje hjul är också en del av konfigurationen av en spelmaskin. På virtuella enarmade banditer och slot spel i nya slot webbplatser, fysiska konfiguration ersättas med parametrisk begränsningar på RNG (random number generator).
För sannolikhet i slots bara en del av parametrar och egenskaper av hela konfigurationen av en slot maskin räknas [. ]. Läs mer om konfigurationer
Vinnande kombinationer, slots händelser
alla vinnande regel på en vinstrad är uttryckt genom en kombination av symboler (till exempel, för att den specifika kombinationen ) eller en typ av kombinationer av symboler (till exempel, alla bar-symbolen två gånger eller valfri trippel symboler) och resultatet är en specifik kombination av hållplatser på den linjen. Därför är kombinationen av hållplatser bör naturligtvis tas som en elementär händelse av sannolikheten området. Vi har möjliga kombinationer av stannar vid En och möjliga kombinationer av symboler på en vinstlinje längd n över n hjulen. I fall B, vi har samma antalet möjliga kombinationer av symboler och möjliga kombinationer av hållplatser för att payline längd n.
Med hänsyn till komplexiteten av händelser i förhållande till mods av sannolikheten beräkningar har vi:
Enkla händelser. Det är dessa händelser som är relaterade till en linje, som är olika typer av kombinationer av hållplatser uttryckt genom särskilda nummer av identiska symboler (instanser). Till exempel, på en vinstlinje längd 3 är en enkel händelse, som definieras som "två sju och en orange symboler".
Komplexa händelser av typ 1. Dessa är fackföreningar enkla händelser som är relaterade till en linje. Till exempel, händelse valfri trippel på en vinstlinje längd 3 av en frukt maskin är en komplex händelse av typ 1, som är unionen av den enkla händelser , , , och så vidare (tänk på att alla symboler som maskinen). Någon dubbel eller två körsbär eller två apelsiner eller minst en av cherry är även komplicerade händelser av typ 1.
Komplexa händelser av typ 2. Dessa är händelser som är olika typer av kombinationer av hållplatser uttryckt genom särskilda nummer av identiska symboler, som är relaterade till flera linjer. Till exempel, på vinstrader 1, 3 eller 5 är en komplex händelse av typ 2-uttryckt genom "två sju och en plommon-symboler". Händelse på minst en vinstraden är också en komplex händelse av typ 2.
Komplexa händelser av typ 3. Dessa är fackföreningar händelser som är olika typer av kombinationer av hållplatser uttryckt genom särskilda nummer av identiska symboler (som komplexa händelser av typ 2), som är relaterade till flera linjer. Till exempel, valfri trippel på vinstrader 1 eller 2 är en komplex händelse av typ 3. Minst ett körsbär på minst en vinstrad är också en komplex händelse av typ 3.
Allmänna formler av sannolikheten för att vinna händelser relaterade till en vinstrad
För att en händelse E rör till en rad längd n, den allmänna formeln för sannolikheten av E är:
I fall A och i fall B (1)
Där F(E) är antalet kombinationer av hållplatser gynnsamt för den händelse E för att förekomma.
För att en händelse E uttrycks i antalet fall av varje symboler på en vinstlinje i fall A, formel (1) motsvarar:
(2)
Där är antalet fall av , och så vidare, är antalet fall av ( ).
Formel (2) kan användas direkt för att vinna händelser som definieras genom distribution av alla symboler på payline, i fall A. Dessa är enkla händelser. För mer komplexa händelser, måste vi tillämpa den allmänna formeln (1), som övergår till att räkna antalet gynnsamma kombinationer av hållplatser F(Eav ), eller, för vissa situationer tillämpas formel (2) flera gånger och lägg till resultaten.
I fall B, antalet variabler är större och därför är de flesta av de explicita formler från fall B är alltför överbelastad. Vi tar här en viss typ av händelser som vi presenterar sannolikheten formel i termer av grundläggande sannolikheter, nämligen de händelser som uttrycks genom ett antal fall av en symbol. Om E är evenemanget exakt m instanser av S ( ), sedan:
(3)
Där och är de grundläggande sannolikheter (sannolikheten av symbol S förekommer på hjul nummer j, respektive k).
Sannolikheten verktyg för händelser som är relaterade till flera rader
för händelser som är relaterade till flera rader, andra egenskaper av sannolikhet används (till exempel, inkludering-exkludering princip), tillsammans med formlerna (1) och (2) och vissa approximativa metoder som är nödvändiga för att underlätta beräkningar. Vid beräkning av sannolikheten för en händelse med anknytning till flera rader, vissa topologiska egenskaper hos denna grupp av linjer räknas; till exempel, självständighet av raderna:
Vi kallar två linjer oberoende om de inte innehåller stannar av samma rulle. Detta innebär att resultatet på en rad beror inte på resultatet av den andra och vice versa. Två linjer som inte är oberoende kommer att kallas icke-oberoende.
För två icke-oberoende linjer, resultatet av en påverkas (delvis eller helt) av resultatet av den andra. Denna definition kan utökas till flera rader (m), som följer: vi kallar m linjer oberoende om varje par av linjer från dem är oberoende. Från probabilistisk synvinkel, helst två eller fler evenemang varje relaterade till en linje från en grupp av oberoende linjer är oberoende i den meningen att den definition av oberoende händelser från sannolikhetsteori.
Oberoende och icke-oberoende rader i en 3 x 3-visning av en 9-hjuls slot maskin
I föregående figur, linjer och är oberoende, medan och , liksom och är icke-oberoende (för de sista två par, de rader som har ett stopp i vanligt).
Icke-oberoende rader i en 4 x 5-visning av en 5-hjuls slot maskin
I föregående figur, linjer och , och , och , och därför , , och , är icke oberoende, eftersom det inom var och en av nämnda grupper har vi stannar i samma rulle på olika linjer. I en sådan konfiguration, det finns ingen grupp av oberoende linjer, oavsett form eller andra egenskaper linjer.
En omedelbar konsekvens av att definitionen av oberoende rader är att om två linjer korsar varandra (de gemensamma hållplatser), de är icke-oberoende, så att någon grupp av rader som innehåller dem kommer att vara icke-oberoende. En annan konsekvens är att om två linjer är oberoende, att de inte korsar varandra.
Om två linjer som inte korsar varandra, de är inte nödvändigtvis oberoende. Till exempel, ta linjer och i den sista figuren. Tvärtom, linjer och inte skär varandra i det sista men en siffra som är oberoende.
Icke-oberoende linjer (korsande eller icke-korsande) för vilka det finns icke-delade stationer hör till samma hjulen (som linjer och i den sista siffran) kallas kopplade linjer. För händelser som är relaterade till kopplade linjer, sannolikheten uppskattningar är endast möjligt om vi vet arrangemang av symbolerna på hjulen, inte bara deras fördelningar.
Alla sannolikheter arbetades fram under följande antaganden:
- hjulen snurrar oberoende av varandra;
- en payline inte innehålla två hållplatser på samma rulle (den korsar över hjulen utan överlappning dem). detta återgår till det faktum att någon m händelser, var och en med anknytning till ett stopp av vinstrad, är oberoende av varandra.
- varje rulle innehåller p symboler, detta är faktiskt en konvention: om en symbol visas inte på en rulle, kunde vi helt enkelt ta sin distribution på den rulle som är noll.
Givna parametrar
naturligtvis, någon praktisk tillämpning kan endast uppfyllas om vi i förväg vet parametrar för given slot maskinen, det är många stannar hjulen och symbolen distributioner på hjulen. Alla sannolikhet formler och tabeller av värderingar är verkningslösa utan den här informationen.
I boken matematik av slots: konfigurationer, kombinationer, sannolikheter du kommer att hitta förklarade några metoder för att uppskatta dessa parametrar baserade på empiriska data som samlats in genom statistisk observation och fysikaliska mätningar. Naturligtvis, med hänsyn till de incomputable fel intervall av sådana approximationer, någon trovärdig information om dessa parametrar bör ha företräde framför dessa metoder för att uppskatta dem.
Matematik institutionen för infarom kommer att lansera inom kort projektet sannolikheten blad för varje slot spel, arbetar med att samla in statistiska uppgifter från slot spelare, att använda data för att skatta parametrarna i den slot maskin, förfina beräkningar med nyinsamlade data och beräkna sannolikheter och andra statistiska indikatorer knutna till utbetalningsschemat av slot maskinen, för att ge den så kallade PAR ark av varje slot spel på marknaden. Kontakta oss med ämne "slots data-projekt" om du vill vara en del av vår framtida projekt.
Praktiska tillämpningar och numeriska sannolikheter
Denna sektion är dedikerad till konkreta resultat, i vilket de allmänna formlerna som preciseras i syfte att ge resultat för de mest vanliga typer av slot spel och vinna händelser. De praktiska resultaten presenteras som både specifika formler, redo för inmatning av parametrar för slot spel, och beräknade numeriska resultat, där den specifika formler tillåta generation av två-dimensionella tabeller med värden. Insamling av resultat som håller för vinnande kombinationer med ingen wild-symbol (joker) och är partiell. Du kan hitta den kompletta samlingen av praktiska resultat i boken matematik av slots: konfigurationer, kombinationer, sannolikheter, för 3-hjuls, 5-hjuls, 9-hjuls, och 16-hjuls spelautomater.
3-hjuls spelautomater
det 3-hjuls slot maskiner kan ha följande vanliga konfigurationer i displayen: 1 x 3 2 x 3 3 x 3. Standard längd på en vinstrad är 3. Den gemensamma vinna händelser på en vinstrad är:
– En särskild symbol tre gånger
(till exempel, ( ))
– någon symbol tre gånger (trippel)
– En särskild symbol exakt två gånger
(till exempel, ( alla))
– någon symbol exakt två gånger (dubbel)
– En särskild symbol exakt en gång
(till exempel, ( alla alla)) |
– en kombination av två specifika symboler
(till exempel, (blanda & ) , som är ( ) eller ( ))
– en kombination av minst en av tre specifika symboler
(till exempel, (alla bar alla bar alla bar ), med tre bar symboler , , )
(symbolerna från exempel är bara för att illustrera den vinnande kombinationerna och kan ersättas med symboler av någon bild. För samma parametrar av maskinen, sannolikheten för att dessa händelser är densamma oavsett vald bild för symboler.)
fackföreningarna vinna händelser på en vinstlinje (avskiljts av tidigare händelser genom , drivs med eller):
8. En särskild symbol minst två gånger
9. En särskild symbol minst en gång
10. En särskild symbol tre gånger eller annan särskild symbol två gånger
11. En särskild symbol tre gånger eller annan särskild symbol en gång
12. En särskild symbol tre gånger eller annan särskild symbol minst en gång
13. En särskild symbol tre gånger eller varje kombination av att symbolen med en annan specifik symbol
14. En särskild symbol två gånger eller annan särskild symbol en gång
15. En särskild symbol dubbelt eller någon kombination av minst en av de tre andra särskilda symboler
På en 3-hjuls 2 x 3 - eller 3 x 3-display slot maskinen, helst två vinstlinjer kopplat därför kan vi inte uppskatta sannolikheter för att vinna händelser relaterade till flera linjer.
16-hjuls spelautomater
den 16-hjuls spelautomater har oftast 4 x 4 konfiguration av displayen. Standard längd på en vinstrad är 4, men det kan också ha den längd 3, 6, 7 eller 8. Den 16-rulle 4 x 4-display slot maskin skulle ha 8 till 22 vinstlinjer av längd 4, som följer: 4 horisontell, 4 vertikalt, 2 sneda (diagonal), eller 12 trapetsformade linjer. Det kan också ha 4 övergripande trappa rader längd 7, 12 dubbel-trappa rader av längd 6 eller 10 dubbel-trappa linjer med längden 8. Det kan också ha 4 sneda linjer längd 3.
Den gemensamma vinna händelser på en vinstrad är:
– En särskild symbol fyra gånger (på en vinstlinje längd minst 4, till exempel, ( ))
– någon symbol fyra gånger (fyra gånger, på en vinstlinje längd minst 4)
– En särskild symbol för exakt tre gånger (på en vinstlinje av längd på minst 3, till exempel, ( alla))
– någon symbol för exakt tre gånger (trippel) (på en vinstlinje av längd på minst 3)
– en kombination av två specifika symboler på en vinstlinje för längd på minst 3, till exempel, (blanda & ) , som är ( ) eller ( ) eller ( en payline av längd 4)
– en kombination av minst en av tre specifika symboler på en vinstlinje för längd på minst 3, till exempel, (alla bar alla bar alla bar alla bar), med tre bar symboler , , , för en payline av längd 4).
Tabellen noter sannolikheten för att vinna händelser på en vinstlinje av längd 4.
Fackföreningarna vinna händelser på en vinstlinje (avskiljts av tidigare händelser genom , drivs med eller):
7. En särskild symbol minst tre gånger
8. En särskild symbol fyra gånger eller annan särskild symbol som tre gånger
9. En särskild symbol fyra gånger eller annan särskild symbol minst tre gånger
10. En särskild symbol fyra gånger eller varje kombination av att symbolen med en annan specifik symbol
11. En särskild symbol tre gånger eller någon kombination av minst en av de tre andra särskilda symboler
Vinnande händelser på flera vinstrader
för sannolikheten för dessa händelser, ansåg vi bara vinstrader av vanlig längd 4 i fall En.
1.1 En vinnande evenemanget på någon av de horisontella linjerna
1.2 En vinnande evenemanget på någon av de vertikala linjerna
1.3 En vinnande evenemanget på någon av de horisontella eller vertikala linjer
1.4 En vinnande händelse om endera eller båda diagonalerna
1.5 En vinnande evenemanget på någon av de horisontella eller diagonala linjer
1.6 En vinnande evenemanget på någon av de vertikala eller diagonala linjer
1.7 En vinnande evenemanget på någon av de horisontella, vertikala eller diagonala linjer
1.8 En vinnande evenemanget på någon av vänster-höger trapetsformade linjer
1.9 En vinnande evenemanget på någon av de horisontella eller vänster-höger trapetsformade linjer
All slots sannolikheter och andra statistiska indikatorer för de mest vanliga typer av slot maskiner och den vanligaste vinna händelser, beskrivs i boken matematik av slots: konfigurationer, kombinationer, sannolikheter . Insamling av sannolikheten resultat presenteras tillsammans med matematiken bakom slot spel. Se böcker avsnitt för mer information. |
|

Se regler och priser i reklamen sida.
Se regler och priser i reklamen sida.
Slot spel matematiker
| |
Alla spel maskiner är konstruerade för att betala spelare tillbaka en del av vad spelas. Beloppen varierar från maskin till maskin och från casino till casino. Alla maskiner har en sak gemensamt: ju längre tid maskinen är spelade, ju närmare den faktiska utbetalningar kommer att vara att de teoretiska resultaten.
Slot maskiner använder ett slumpmässigt urval process för att uppnå en uppsättning teoretiska odds. Slumpmässigt urval innebär att varje gång spaken dras och hjulen sätts i rörelse av en kombination av symboler är slumpmässigt utvalda. Den "slumpmässiga" aspect garanterar att varje dra i handtaget är oberoende från alla andra dra, så att resultaten av den föregående dra, och den innan det, har ingen effekt på den nuvarande.
Den teoretiska odds är inbyggd i konstruktion och program i maskinen, och det är möjligt att beräkna den exakta utbetalningsprocent för varje maskin på lång sikt.
Med undantag för den video slots, spelautomater har hjul som kallas rullar med symboler tryckta på varje hjul. Varje rulle symbol representerar ett stopp som kan komma att vila på payline, och kan eller inte kan vara en del av en kombination av symboler resulterar i en payoff.
Sannolikheten för att vinna någon utdelning på varje slot maskin är relaterade till antalet rullar och antalet symboler på varje hjul.
Den vanligaste typen av mekaniska slot maskinen har tre rullar med tjugo-symboler på varje hjul. För att beräkna det totala antalet kombinationer av symboler på denna maskin, vi flera antalet stopp (symboler) på varje rulle med antalet stannar på var och en av de återstående hjulen. För en tre hjuls maskinen med tjugo stationer per rulle, vi har 20 x 20 x 20 = 8000 kombinationer av slot symboler.
Om en jackpot som erbjuds på den här maskinen betalar den 7 7 7 och bara en 7-symbol på varje rulle, då sannolikheten för att träffa denna jackpot är 1/20 x 1/20 x 1/20 eller en på 8 000. Om två 7-symboler på en rulle, då vår beräkning är 2/20 x 1/20 x 1/20 för en sannolikhet 1/4,000 för att träffa jackpotten.
På samma sätt kan vi beräkna sannolikheten för varje kombination av symboler för att slå om vi vet hur många gånger varje symbol visas på varje rulle.
När mekaniska slots dominerade, var det inte alltför svårt att räkna de symboler på varje hjul och bestämma exakt payoff för en viss maskin. Med mikroprocessor kontrollerad slots denna uppgift har blivit nästan omöjligt, eftersom antalet stopp per rulle kan vara så många som 256. För att fastställa utdelningen av en sådan maskin skulle kräva betydande reverse engineering och är utanför omfånget för nästan alla spelare.
Hur många hjul har en större effekt på sannolikheter än det antal symboler per rulle. Om vi jämför en maskin med 32 stationer per hjul och 3 rullar, med en 22-stopp per rulle maskinen och 4 hjulen, kommer du att se den enorma skillnaden annan rulle gör:
32 stop, 3 hjul: 32 x 32 x 32 = 32,768 kombinationer
22 stoppa, 4 rulle: 22 x 22 x 22 x 22 = 234,256 kombinationer
Om vi betraktar en 5-hjuls maskin med 32 stationer per rulle, finner vi över 33 miljoner kombinationer!
Varje maskin har en förutbestämd utbetalningsprocent. När du hör saker som "våra slots betala tillbaka till 98,3%", detta betyder att på lång sikt för varje dollar som sitter i maskinen, kommer den att återgå till 98,3 cent. Omvänt, kan vi konstatera att för varje dollar som spelas, kasino kommer att behålla 1,7 cent. Dessa procentsatser endast att gälla under mycket lång sikt spela som består av hundratusentals eller miljontals spelar.
Många människor misstolkar dessa procentsatser och tror att om de spelar med $100.00 på 98.3% återbetalning maskinen att de bara kan förlora $1.70. Det finns ett par saker som är fel med denna tankegång. För det första, teoretiska procenttal kommer att uppnås endast under långa perioder av att spela. Över ett par dussin, eller ens ett par hundra rullar, avkastning procent kommer att variera kraftigt. För det andra, om en person tar $100.00 för slot spela, han eller hon vanligtvis inte kommer att begränsa hans eller hennes pjäs att sätta in detta belopp av pengar i maskinen endast en gång. De flesta människor kommer att köpa tjugo dollar värt av polletter och fortsätta att spela med dessa pengar tills det är borta. Efter insättning av den första omgången av mynt i maskinen, de kommer att fortsätta spela med några mynt kvar i facket, och de kommer att fortsätta med detta mönster tills inga mynt kvar. Och sedan undrar de över hur det var möjligt för en till 98,3% slot att ta alla sina pengar.
Svaret är att kasinot fortsätter att extrahera dess andel på varje mynt sätts in i maskinen. Den spelare som inte kommer att begränsa hans spel till tjugo dollar eller hundra dollar men kommer att fortsätta att pågående mynt. Maskinen kommer att, åtminstone på lång sikt, fortsätter att slipa bort alla pengar spelas.
Tabell 6 visar de förödande effekt på huset kanten kan ha på spelarens spelkonto. Denna tabell jämförs slot håll procentsatser av från två procent till femton procent för tio omgångar av spel, från och med $100.
Tabell 6. Belopp per spelomgång
Slot maskinen matematik: utforska spelet odds och träffa frekvens
Slot maskiner är mycket enkelt att spela och kräver inte några särskilda spel kunskaper. Vem som helst kan få i spelet. Varje dragning är precis som alla andra spin – de är alla helt random. Men bara för att de är slumpmässiga betyder inte att det finns ingen matematik. Alla maskiner har en sak gemensamt – ju längre du spelar, desto närmare kommer utbetalningen att ske till teoretiska resultat.
Men för att förstå den teoretiska odds är det viktigt att förstå lite mer om träff frekvens och avkastning procent.
Klassiska slots och klassiska odds
Tekniken av slot maskiner kan ha förändrats över åren, men spelet har förblivit detsamma. En spelare sätter in en slant och drar i handtaget för att rotera en serie av rullar. Varje rulle har en bild eller symbol tryckt på dem. Beroende på vilka bilder som ställer upp med vinstlinje, vinner du. Och utbetalningen beror på vilka bilder som radas upp.
Den klassiska mekaniska slot maskiner som används springs och spänning för att stoppa hjulen på måfå. Dessa gamla elektro-mekaniska slots var inte längre förutsägbart än dagens moderna slots. De flesta gamla mekaniska maskinerna hade tre hjul som hölls 20 symboler, medan de flesta moderna slots har tre virtuella hjulen med 22 stationer och en random number generator program.
Till exempel, för en gammal spelautomat med 20 stannar på varje hjul det skulle vara 8000 olika kombinationer. Vi får detta nummer genom att multiplicera antalet symboler på varje hjul (20 x 20 x 20 = 8000). De 8 000 möjliga kombinationer är känd som en cykel. Det är viktigt att veta att cykeln inte betyda cykeln för att vinna och förlora – bara den matematiska cykel.
I teorin, om du dragit i spaken 8000 gånger, skulle du se att varje kombination av hjulen en gång. För att räkna ut oddsen för att träffa en viss kombination av tre hjul, bara multiplicera dina chanser att landa en symbol av sig själv (1/20 x 1/20 x 1/20). Detta innebär att dina odds för att dra upp någon kombination på en klassisk slot maskinen är på 1/8 000 7999 till 1.
Precis som med vända ett mynt – oddsen kan vara 50/50, men du kommer sannolikt inte att se exakt 50 huvuden och exakt 50 svansar om du vänt ett mynt 100 gånger. Men med både en slot-maskin eller en coin flip, det högre antalet gånger du gör det, desto närmare odds skulle vara att de faktiskt sannolikhet. Så för att faktiskt komma nära dem som odds, skulle du behöva vända på mynt miljoner eller miljarder gånger.
Hur slumpmässiga nummer generatorer arbete
Moderna spelautomater är mer komplicerad, är det mycket svårare att matematiskt förutsäga oddsen, eftersom siffrorna är teoretiska och är i huvudsak utvecklats från en pool av oändlig spins.
Moderna spelautomater använda sig av en random number generator (RNG). RNG elektroniskt genererar ett slumpmässigt värde från miljontals kombinationer. Dessa värderingar är avgörande för där rullen stannar. Elektroniska spelautomater generera dessa siffror i en takt av 300-500 per sekund. När du trycker på "spin" - knappen på en elektronisk spelautomat, den behandlar slumpmässiga värden. Det första värdet som det väljer bestämmer positionen för den första rullen, det andra värdet för den andra rullen och det tredje värdet för den tredje rullen.
En maskin payback procent är hur många procent maskinen kommer att "betala tillbaka" till spelaren i det långa loppet. Återbetalningstiden procent är programmerat i maskiner av tillverkarna och kan justeras beroende på hur lös den casino vill slots att vara. Maskiner med en högre avkastning procent är vanligen betecknas som "loss".
De flesta maskiner kör en payback procent någonstans mellan 75 och 99 procent. Till exempel, om en slot maskinen har en 90percent payback, det kommer teoretiskt att betala tillbaka 90 cent på varje dollar som betalas i. Tänk på att dessa procentsatser är räknat från en oändlig pool snurrar.
Säg att du ser en annons för ett kasino med en 95percent payback. Vad detta egentligen säger är att "du sätter in $100 så ger vi dig tillbaka $95." naturligtvis, kan du vinna stort på den första dollar eller förlora alla $100. Tänk tillbaka på ett slumpmässigt coin flip – du har en 50/50 chans att vinna. I en helt bara spel där casinot inte har någon fördel, du satsar $100 och vinner får du 100 kr och om du förlorar du förlorar $100. Teoretiskt är över tillräckligt med tid, du och casino skulle vara ännu.
Men med 95 procent avkastning, kasinot i huvudsak betalar du $95 för din vinst men ändå tar de $100 när du förlorar. I detta scenario du att förlora $5 för varje $100 du satsar. Det är hur ett kasino vinna mindre vinster än pengar spelat och förlorade.
Frekvensen är den teoretiska andelen spins som kommer utbetalning något till spelaren. Frekvensen är baserat på hur många gånger varje symbol visas samt hur ofta vinnande kombination uppstår. Maskiner med hög träff frekvenser som betalar ut små vinster oftare och maskiner med lägre hit frekvenser betala ut mindre ofta, men med mer pengar.
Träff frekvens i princip talar om för dig hur många gånger du måste förlora för att vinna – i genomsnitt. En återgång av ett par av mynt är en hit, men det är inte mycket av en vinst. För de flesta slot machines, träff frekvens varierar från 9 till 25 procent. Det visar sig att en träff i genomsnitt 9-25 gånger för varje 100 spins som bedrivs. Dessa träffar kan vara allt från en marginell avkastning till en enorm utbetalning.
Det är viktigt att notera att det oftast finns någon direkt korrelation mellan utbetalningsprocent och träffa frekvens. Maskiner med hög payback kan fortfarande ha ett lågt träff frekvens eller vice versa. En maskin med hög avkastning och låga hit frekvens innebär att det inte träffar så ofta, men det betalar ut mer. En maskin med låg avkastning och hög träff frekvens betalar ut små vinster, mer ofta.
Så oavsett om du njuta av att vänta längre för större utbetalning eller få lite avkastning och mindre väntetid, du kommer nu att kunna hitta en spelautomat som är den perfekta kombinationen av underhållning och vinst.
[ftctabox boxstyle="6" buttonstyle="3" linkurl="http://www.Casinosonline.Com/casino-games/slots/" buttontext="gå hit för bästa slots kasinon" buttonalt="besöka våra slots avsnitt logourl="http://www.Casinosonline.Com/wp-content/uploads/2013/05/play-online-slots.Jpg" buttonalign="center" logoalign="left"]
Högst rankade slots online
Vi har granskat och betygsatt några av de bästa online kasinon för slots. Massor av stora, exklusiva bonusar och kampanjer för både nya och erfarna spelare. AMERIKANSKA spelare är välkomna![/ftctabox]
Slot spel matematiker
Denna guide, skriven av casino matematik professor robert hannum, innehåller en kort icke-teknisk diskussion om den grundläggande matematik som reglerar casino spel och visar hur kasinon tjäna pengar på dessa spel. Artikeln tar upp en mängd olika ämnen, inklusive hus fördel, förvirring, om att vinna priser, spel volatilitet, spelare värde och comp politik, casino prissättning misstag, och regulatoriska frågor. Statistiska fördelar som är förknippade med stora spel också.
|
| Förståelse casino matematik |
- Introduktion
- Varför är matematik viktigt?
- Huset kanten
- Sannolikheten kontra odds
- Förvirring om vinner priser
- Volatilitet och risk
- Spelaren värde och complimentaries
- Gaming förordning och matematik
- Sammanfattande tabeller för husets fördel
Kärnan i verksamheten av casino spel är ganska enkel. Kasinon tjäna pengar på sina spel på grund av matematiken bakom spel. Som nico zographos, återförsäljare-extraordinaire för den "grekiska syndicate" i deauville, cannes och monte carlo på 1920-talet observerade om casino spel: "det finns ingen sådan sak som lycka. Det är allt matematik."
Med några anmärkningsvärda undantag, huset alltid vinner i det långa loppet - på grund av den matematiska fördel casinot har över spelaren. Det är vad mario puzo syftade på i sin berömda roman de oförnuftiga dö när hans fiktiva casino boss karaktär, gronevelt, kommenterade: "procentsatserna aldrig ljuga. Vi har byggt alla dessa hotell på procentsatser. Vi stannar rika på procentandelen. Du kan tappa tron på allt, religion och gud, kvinnor och kärlek, godhet och ondska, krig och fred. You name it. Men andelen kommer alltid stå fast."
Puzo är, naturligtvis, rätt på pengarna om casino spel. Utan den "kanten", kasinon inte skulle existera. Med denna kant, och på grund av en berömda matematiska resultat som kallas de stora talens lag, ett kasino är garanterad att vinna i det långa loppet.
Varför är matematik viktigt?
Kritiker av gaming industrin har länge anklagat det för att skapa namn för "gaming" och använda detta som mer politiskt korrekt än att ringa själv "spelindustrin." begreppet "spel" men, har varit runt i århundraden och mer exakt beskriver aktörernas syn på branschen för att oftast casino operatörer är inte spel. I stället förlitar de sig på matematiska principer för att säkerställa att deras anläggning genererar positiva bruttointäkter. Operatören måste dock försäkra spelintäkterna är tillräckliga för att täcka avdrag som osäkra fordringar, kostnader, avgifter, skatter och räntor.
Trots det uppenbart att många casino proffs begränsa sina framsteg genom att underlåta att förstå grundläggande matematik spel och deras relationer till casino lönsamhet. En kasino ägare ofta skulle testa sin pit chefer genom att fråga hur en casino kunde tjäna pengar på blackjack om utfallet bestäms helt enkelt av om spelaren eller dealern kom närmast 21. Svaret, typiskt, var att casino upprätthålls "ett hus fördel." detta var fair enough, men många kunde inte fastställa beloppet av den nytta eller vilken aspekt av spel som skapats fördel. Med tanke på att de produkter som erbjuds av casinon är spel, chefer måste förstå varför de spel som ger de förväntade intäkterna. I gaming industrin, ingenting spelar en viktigare roll än matematik.
Matematik bör också övervinna faran med vidskepelse. En ägare av en stor las vegas strip casino gång upplevt en strimma av att förlora stora summor pengar till några "high rollers." han inte tillskriva denna förlorande strimma till normal volatilitet i spel men otur. Hans lösning var enkel. Han tillbringade kvällen sprida salt i hela kasinot för att jaga bort onda andar. Innan du tillskriver detta exempel egenheterna hos en ägare, hans är atypiska bara i deras extrema. Vidskepelse har länge varit en del av spel - från båda sidor av bordet. Vidskepelse kan det leda till irrationella beslut som kan skada kasino vinster. Till exempel, anta att en viss återförsäljare, är otur mot en viss (vinnande) spelaren kan leda till ett beslut om att ändra återförsäljarna. Lika många, om inte de flesta spelare är vidskepliga. I bästa fall kan han ogillar att kasinot är att försöka ändra sin lycka. I värsta fall får spelaren att känna nya återförsäljare är utbildad i metoder för att "coola" spelet. Kanske han är även bekant med historier om gamla där kasinon är anställd återförsäljare att fuska "tur" - spelare.
Att förstå matematik i ett spel som också är viktigt för kasinot operatören att se till att rimliga förväntningar på spelarna är uppfyllda. För de flesta personer, spel är underhållning. Det ger ett utlopp för vuxna spela. Som sådana personer har möjlighet att för en trevlig avledning från det vanliga livet och från samhälleliga och personliga påfrestningar. Som en underhållning alternativ, men spelare kan överväga värdet av spelupplevelse. Till exempel, vissa människor kan ha möjlighet att antingen tillbringa en hundra dollar under en kväll genom att gå till en professionell basket spel eller på en licensierad kasino. Om huset fördel är för stark och den person som förlorar sina pengar för snabbt, kan han inte värde som kasino underhållning erfarenhet. Å andra sidan, om en casino kan roa honom för en kväll, och han har ett "gratis" mat eller dryck, han kanske vill upprepa upplevelsen, även över en professionell basket spel. Likaså kan nya casino spel själva kan lyckas eller misslyckas baserat på spelarnas förväntningar. Under de senaste åren, kasinon har debuterade en rad nya spel som försök att vinna spelare intresse och hålla kvar deras uppmärksamhet. Oavsett om ett spel är roligt och intressant att spela, oftast en spelare inte vill spela spel där hans pengar försvinner alltför snabbt, eller där han har en ovanligt avlägsen chans att återvända hem med vinster.
Matematiken spelar också en viktig del i att möta spelarnas förväntningar som de tänkbara följderna av hans gambling-aktiviteter. Om spelandet innebär ett rationellt beslutsfattande, skulle det vara irrationellt att satsa pengar där din motståndare har en bättre chans att vinna än vad du gör. Adam smith föreslog att alla spel om pengar, där operatören har en fördel, är irrationella. Han skrev "det finns inte, dock en viss proposition i matematik än att fler biljetter [i ett lotteri] du annonsera på, desto mer sannolikt att du är en förlorare. Äventyr på alla lotter i lotteriet, och du förlorar för vissa, och ju större antal biljetter, ju närmare du närma dig till denna visshet."
Även där huset har en fördel, men en spelare kan vara motiverat om det förlorade beloppet betyder mycket för honom, men den potentiella vinsten skulle upphöja honom till en högre stående levande. Till exempel, en person med en årsinkomst på 30 000 dollar kan ha $5 i disponibel weekly intäkter. Han kunde spara eller spela detta pengar. Genom att spara den i slutet av ett år skulle han ha $260. Även om han gjorde detta för ett år sedan besparingar skulle inte höja sin ekonomiska status till en annan nivå. Som ett alternativ, han kunde använda $5 att spela för chansen att vinna $1 miljon. Medan oddsen för att vinna är avlägsna, det kan utgöra den enda möjligheten att flytta till en högre ekonomisk klass.
Eftersom casino industrin är hårt reglerade och vissa av de normer som fastställs av tillsynsorgan innebär matematiskt relaterade frågor, casino chefer bör också förstå den matematiska aspekter som rör gaming förordning. Gaming förordning är främst tillägnad för att försäkra dig om att spel som erbjuds i kasinot är rättvisa, ärlig, och att spelarna får betalt om de vinner. Rättvisa är ofta uttryckt i föreskrifter som antingen kräver en minsta avkastning till spelaren eller i mer extrema fall, som dikteras av den faktiska reglerna för de spel som erbjuds. Casino befattningshavare bör förstå den inverkan som regler förändringar har på återbetalning till spelarna för att säkerställa att de uppfyller lagstiftningen. Lika viktigt, casino befattningshavare ska förstå hur regeringen i uppdrag regler skulle påverka deras gaming intäkter.
Spelarens chanser att vinna i ett casino spel och i vilken takt han vinner eller förlorar pengar beror på spelet, regler i kraft för just det spelet, och för vissa spel sin nivå av skicklighet. Hur mycket pengar spelare kan förvänta sig att vinna eller förlora i det långa loppet - om satsning görs om och om igen - kallas spelarens satsning förväntade värdet (EV), eller förväntan. När spelarens satsning förväntan är negativ, att han kommer att förlora pengar i det långa loppet. För en 5 $satsning på den röda färgen i roulette, till exempel, förväntan är -$0.263. Om den genomsnittliga spelaren kommer att förlora drygt en fjärdedel för varje $5 satsa på rött.
När insatsen förväntan ses från casino perspektiv (jag.E., den negativa av spelarens förväntningar) och uttrycks som en procentsats, har du husets fördel. Till exempel roulette, huset kanten 5,26% ($0.263 dividerat med $5). Den formella beräkning är följande:
EV = (+5)(18/38) + (-5)(20/38) = -0.263
(husets fördel = 0.263/5 = 5.26%)
När detta EV-beräkningen görs för en 1-enhet uppgår det negativa i det resulterande värdet är huset kanten. Här är beräkningarna för spel på ett enda nummer i dubbel-noll och single-zero roulette.
Dubbel-noll roulette (single number bet):
EV = (+35)(1/38) + (-1)(37/38) = -0.053
(husets fördel = 5.3%)
Single-zero roulette (single number bet):
EV = (+35)(1/37) + (-1)(36/37) = -0.027
(husets fördel = 2.7%)
Husets fördel representerar det långa loppet andel av satsade pengar som kommer att behållas av casino. Det är också kallas hus kanten, den "odds" (jag.E., undvik spel med dåliga odds), eller bara "procent" (som i mario puzos de oförnuftiga dö). Även om huset kanten kan lätt räknas för vissa spel, till exempel, roulette och craps - för det andra kräver mer avancerad matematisk analys och/eller datorsimuleringar. Oavsett vilken metod som används för att beräkna det, husets fördel motsvarar det pris till spelare för att spela spelet.
Eftersom denna positiva hus kanten finns för i stort sett alla spel på ett casino (ignorerar poker rum och sport, där ett fåtal medarbetare kan göra en levande), spelare står inför en uppförsbacke, och i det långa loppet, förlorar slaget. Det finns några undantag. Oddsen i craps har noll hus kanten (även om denna satsning kan inte göras utan att en annan negativ förväntan satsning) och det finns några video poker maskiner som avkastning är större än 100 procent om det spelas med perfekt strategi. Ibland casino kommer även erbjuda en kampanj som ger kloka spelare en positiv förväntan. Dessa erbjudanden är oftast fel - ibland kasinon inte kontrollera matematik - och avslutas när casino inser spelare har kant. Men på det stora spelare kommer att förlora pengar i det långa loppet, och huset kanten är ett mått på hur snabbt pengarna kommer att gå förlorade. En spelaren som satsar i ett spel med 4% hus fördel tenderar att förlora sina pengar dubbelt så snabbt som en spelare gör satsningar med en 2% hus kanten. Tricket för att intelligenta kasino spel - åtminstone från den matematiska förväntan synvinkel - är att undvika spel och spel med den stora hus fördelar.
Vissa casino spel är en ren slump - ingen mängd av skicklighet eller strategi kan ändra oddsen. Dessa spel är roulette, craps, baccarat, keno, big six wheel of fortune, och spelautomater. Av dessa är baccarat och craps erbjuder de bästa oddsen, med hus fördelarna med 1,2% och mindre än 1% (om man endast räknar med pass/come med full odds), respektive. Roulette och slots kostnad spelaren mer - huset fördelar med 5,3% för dubbel-noll roulette och 5% till 10% för slots - när lyckohjulet flöden casino nära 20% av satsningar, och keno är en veritabel casino cash cow med genomsnittligt hus fördel nära 30%.
Spel där en del skicklighet kan påverka husets fördel inkluderar blackjack, video poker, och de fyra populära poker-baserade bordsspel: caribbean stud poker, let it ride, three card poker och pai gow poker. För det poker spel, optimal strategi resulterar i ett hus kanten på 3% till 5% intervall (CSP har det största huset kanten, PGP den lägsta, med LIR och TCP i mellan). För video poker den statistiska fördel varierar beroende på maskin, men i allmänhet det här spelet kan vara mycket spelare vänlig - hus kanten mindre än 3% är inte ovanligt, och vissa är mindre än 1% - om det spelas med strategi expert.
Blackjack, mest populära av alla bord spel, erbjuder skickliga spelare några av de bästa oddsen i kasinot. Huset kanten varierar något beroende på vilka regler och antal däck, men en spelare med hjälp av grundläggande strategi ansikten liten eller ingen nackdel i en enda kortlek och endast 0,5% hus kanten i en gemensam sex-däck spel. Trots dessa siffror, är den genomsnittliga spelaren slutar ge casino en 2% kanten på grund av misstag och avvikelser från grundläggande strategi. Komplett grundläggande strategi tabeller kan hittas i många böcker och många kasino-hotell eller butiker som säljer färg-kodade kreditkort storlek versioner. Variationer av regler som gynnar spelaren finns färre däck, dealern står på en mjuk sjutton (värt 0.2%), en fördubbling efter delning (0.14%), sen surrender (värde uppgår till 0,06 procent), och tidigt överlämnande (ovanligt, men det är värt att 0.24%). Om återförsäljare träffar mjuk sjutton det kommer att kosta dig, så kommer några begränsningar för när du kan dubbla.
Sannolikheten representerar det långa loppet förhållandet (# gånger en utfallet inträffar) för att (# gånger försöket är genomfört). Odds representerar det långa loppet förhållandet (# gånger ett utfall inte inträffar) (# gånger en utfallet inträffar). Om ett kort är slumpmässigt utvalda från en vanlig kortlek med 52 spelkort, sannolikheten att det är en spade är 1/4, odds (mot spade) är 3 till 1. Den verkliga oddsen för att en händelse utgör den utdelning som skulle göra den satsning på evenemanget rättvis. Till exempel kan en satsning på ett enda nummer i dubbel-noll roulette en sannolikhet för 1/38, så för att bryta även på lång sikt en spelare som skulle betalas 37 till 1 (den faktiska utdelningen är 35 till 1).
Det finns alla typer av procentsatser i världen av spel. Vinstprocent, teoretiska vinstprocent, håll procent, och husets fördel kommer att tänka på. Ibland casino chefer använda dessa procenttal på samma sätt, som om de är bara olika namn för samma sak. Visserligen kan det i vissa fall är korrekt. Huset kanten är bara ett annat namn för teoretiska vinna procent och för spelautomater, håll andelen är (i princip) motsvarande för att vinna procentsats. Men det finns grundläggande skillnader mellan dessa vinna priser avstånd.
Husets fördel - den stora andelen som förklarar hur kasinon tjäna pengar - också kallas hus kanten, den teoretiska vinna procent och förväntas vinna procentsats. På dubbel-noll roulette, denna siffra är 5,3%. På lång sikt huset kommer att behålla 5,3% av de pengar som satsas. På kort sikt, naturligtvis, själva vinna andel skiljer sig från de teoretiska vinna andel (omfattningen av denna avvikelse kan förutsägas från statistisk teori). Den faktiska vinstprocent är bara den (verkliga) vinst dividerat med handtag. På grund av de stora talens lag - eller som vissa föredrar att kalla det, lagen i genomsnitt - som antalet prövningar blir större, den faktiska vinna procentsats bör komma närmare den teoretiska vinstprocent.
Eftersom handtaget kan vara svårt att mäta för bords spel, prestanda mäts ofta genom att hålla procent (och ibland felaktigt kallas win procent). Håll andelen är lika för att vinna dividerat med släpp. I nevada, denna siffra är ca 24% för roulette. Släpp ned andel påverkas av många faktorer; vi kommer inte att gräva i dessa eller de associerade administrativa frågor. Det räcker med att säga att casino inte kommer att på lång sikt hålla 24% av de pengar som satsat på de snurr på roulette hjulet - ja, en ärlig casino kommer inte.
För att sammanfatta: husets fördel och teoretiska vinna andel är samma sak, håll är andelen vinna över släppa, vinstprocent är att vinna över handtaget, vinna procent metoder husets fördel eftersom antalet spel ökar, och håll andel är motsvarande att vinna procentsats för slots men inte bordsspel.
· håll % = vinst/drop
· vinna % (faktiska) = win/handtag
· H. A. = teoretisk vinna % = max(faktiska vinna %) = övre gräns(win/handtag)
· håll andel 1 huset kanten
Dessutom har huset en fördel är själv föremål för olika tolkningar. I let it ride, till exempel, är kasinot fördel, antingen med 3,51% eller 2.86% beroende på om du uttrycka fördelen med avseende på basen satsa eller den genomsnittliga insatsen. De som är bekanta med spelet vet att spelare börjar med tre lika stora bas satsningar, men kan dra tillbaka ett eller två av dessa ursprungliga enheter. Det slutliga belopp som placeras på risk, då kan det vara en (84,6 procent av tiden antar rätt strategi), två (8.5%), eller tre enheter (6,9 procent), vilket gör att den genomsnittliga insats storlek 1.224 enheter. I det långa loppet, kasinot kommer att vinna med 3,51% av händerna, vilket motsvarar 2.86% av de pengar som satsas. Så vad är huset kanten för let it ride? Vissa föredrar att säga med 3,51% per hand, andra 2.86% per enhet som satsas. Det spelar ingen roll. Hursomhelst, den nedersta raden är samma i båda fallen: förutsatt att tre $1 bas spel, casino kan förvänta dig att tjäna 3.5¢ per hand (observera att 1.224 x 0.0286 = 0.035).
Frågan om att använda basen insats eller genomsnittliga insats storlek uppstår också i caribbean stud poker (5.22% vs. 2.56%), three card poker (3.37% vs. 2.01%), casino war (2.88% vs. 2.68%) och röda hund (2.80% vs. 2.37%).
För ytterligare andra spel huset kanten kan anges med eller utan band. De främsta exemplen här är de spelare (1.24% vs. 1.37%) och banker (1.06% vs. 1.17%) satsningar i baccarat, och don ' t pass-satsning (1.36% jämfört med 1,40 procent) i craps. Igen, dessa är olika syn på kasinot kanten, men de förväntade intäkterna kommer inte att ändra.
Att huset fördel kan visas i olika förklädnader kan vara oroande. När den är korrekt beräknad och tolkas, men oavsett vilken representation som är vald, samma sanning (läs: pengar) framträder: förväntade vinst är densamma.
Statistisk teori kan användas för att förutsäga omfattningen av skillnaden mellan den faktiska vinna procent och de teoretiska vinna procentsats för ett visst antal satsningar. När observera den faktiska vinstprocent en spelare (eller casino) kan uppleva, hur mycket variation från teoretiska vinna kan man förvänta sig? Vad är en normal variation? Underlag för analysen av sådan volatilitet frågor är ett statistiskt mått som kallas standardavvikelsen (i huvudsak den genomsnittliga avvikelsen för alla möjliga utfall från den förväntade). Tillsammans med den centrala gränsvärdessatsen (en form av stora talens lag), standardavvikelse (SD) kan användas för att bestämma konfidensintervallet med följande volatilitet riktlinjer:
Volatilitet analys riktlinjer
· endast 5% av tiden kommer resultaten kommer att vara mer än 2 SD: s från förväntade resultat
· nästan aldrig (0.3%) kommer resultaten att vara mer än 3 SD: s från förväntade resultat
Naturligtvis är en nyckeln till att med hjälp av dessa riktlinjer är värdet av SD. Design SD-värde ligger utanför ramen för denna artikel, men för att få en idé bakom konfidensintervallet, överväga en serie om 1000 pass line satsningar i craps. Eftersom varje insats har en 1,4% hus fördel, i genomsnitt spelare kommer att vara kvar av 14 enheter. Det kan vara visas (beräkningar utelämnas) att satsa standardavvikelse är ett enda pass line bet är 1.0, och för 1 000 satsningar SD är 31.6. Tillämpning av volatiliteten riktlinjer, kan vi säga att det är 95% chans att spelaren faktiskt vinna kommer att vara mellan 49 enheter vidare och 77 enheter bakom, och nästan säkert mellan 81 enheter vidare och 109 enheter bakom.
En liknande analys för 1 000 enda nummer satsningar på dubbel-noll roulette (i genomsnitt spelaren kommer att vara bakom 53 enheter, satsa SD = 5.8, 1,000 satsning SD = 182.2) kommer avkastningen 95% konfidensintervall på spelaren vinner 311 enheter vidare och 417 enheter bakom, med att vinna nästan säkert mellan 494 enheter vidare och 600 enheter bakom.
Observera att om volatiliteten analys görs i termer av den andel av vinst (snarare än antalet enheter eller beloppet som du har vunnit), konfidensintervallet kommer att konvergera till huset fördel som antalet insatser ökar. Detta är resultatet av de stora talens lag - som antalet prövningar blir större, den faktiska vinna procentsats bör komma närmare den teoretiska vinna procentsats. Risken i spelbranschen beror på bankens fördel, standardavvikelse, insats storlek och längd spela.
Spelaren värde och complimentaries
Med hjälp av husets fördel, insatsens storlek, varaktighet spela, och takten i spelet, i ett kasino kan avgöra hur mycket man förväntar sig att vinna från en viss spelare. Denna spelare att tjäna potential (även kallad player värde, spelare värt, eller teoretiska vinna) kan beräknas med formeln:
Intjäningsförmåga = genomsnittlig insats timmar spelade beslut per timme husets fördel
Till exempel, antag att en baccarat spelare satsar $500 per hand för 12 timmar vid 60 händer per timme. Med ett hus fördel på 1,2 procent, den här spelaren är värt att casino är $4,320 (500 12 60 .012). En spelare som satsar $500 per spinn för 12 timmar på dubbel-noll roulette på 60 spins per timme skulle vara värt omkring $19,000 (500 12 60 .053).
Många kasinon som comp (gratis) politik genom att ge spelaren tillbaka en fast procentsats av sin intjäningsförmåga. Även om comp och rabatten politik som bygger på teoretisk förlust som är mest populära, rabatter på faktiska förluster och död chip program används också i vissa kasinon. Vissa program innehålla en blandning av system. Den matematik som är förknippade med dessa program kommer inte att behandlas i denna artikel.
I ett försök att locka spelare och öka affärer, kasinon då och då erbjuda nya satsningar, sidan satsningar, ökade satsningar, eller variationer av regler. Dessa kampanjer har effekten av att sänka husets fördel och det effektiva priset av spelet för spelaren. Detta är sunt resonemang från en försäljning synvinkel, men kan vara förödande för casino om vård vidtas för att garantera matematik bakom kampanjen är sund. En casino erbjuds en baccarat provision på vinnande bank satsningar på endast 2% i stället för de vanliga 5%, vilket resulterar i en 0.32% - spelare fördel. Detta är lätt att se (med kända sannolikheter för att vinna och förlora banken insats):
EV = (+0.98)(.4462) + (-1)(.4586) = 0.0032
(husets fördel = -0.32%)
Ett casino i biloxi, mississippi gav spelarna en 12,5% kanten på sic bo satsningar av den 4 och 17 år när de erbjöd 80 till 1 utdelningen i stället för de vanliga 60-till-1. Återigen, detta är en enkel beräkning. Med hjälp av det faktum att sannolikheten för att rulla fram en summa av 4 (samma beräkning gäller för totalt 17) med tre tärningarna är 1/72 (1/6 x 1/6 x 1/6 x 3), här är de förväntade värdena för både den vanliga och den pr-satsningar:
Vanliga 60 till 1 i utbetalning: EV = (+60)(1/72) + (-1)(71/72) = -0.153
(husets fördel = 15.3%)
Pr-80 till 1 i utbetalning: EV = (+80)(1/72) + (-1)(71/72) = +0.125
(husets fördel = -12.5%)
I andra pr-fadäser, illinois flodbåt kasino förlorat ett rapporterat $200,000 på en dag med sin "2 till 1 tisdagar" att betalda spelare 2 till 1 (den vanliga utbetalningen är 3: 2) om blackjack naturals, en ordning som gav spelare en 2% fördel. För att inte överträffas, en indisk casino i kalifornien betalt 3 till 1 på naturals under deras "happy hour", offrade tre gånger om dagen, två dagar i veckan i över två veckor. Den här kampanjen gav spelaren en jättestor 6% kanten. En liten casino i las vegas erbjuds en blackjack regel variant som kallas "free ride" där spelarna fick en gratis höger-till-överlämnande token varje gång de fått en naturlig. Korrekt användning av token har lett till en spelare kanten på 1,3 procent, och casino förlorade uppskattningsvis 17 000 dollar i åtta timmar. Ett annat stort casino i las vegas erbjuds en "50/50 split" blackjack sida satsning som tillät spelare att stå på ett ursprungligt innehav av 12-16, och börja en ny hand för lika insatser mot samma återförsäljare upp kort. Även om spelet marknadsförare hävdade variationen var till fördel för kasinot, visade det sig att spelare som utövas 50/50 split endast mot dealern 2-6 hade en 2% fördel. Enligt en pit boss casino drabbades av en $230,000 förlust i tre och en halv dagar.
I spelbranschen, det handlar om att "dåliga matte" eller "bra matematik." ärligt spel baserade på bra matte med positiva husets fördel minimera riskerna på kort sikt, och säkerställa att casinot kommer att tjäna pengar i det långa loppet. Spelare kommer att få "lucky" på kort sikt, men som är en del av grand design. Fluktuationer i båda riktningarna kommer att inträffa. Vi kallar dessa svängningar bra tur eller otur beroende på riktningen av fluktuationer. Det finns ingen sådan sak som lycka. Det är alla matematik.
Gaming förordning och matematik
Casino spel är en av de mest reglerade branscher som finns. Mest spel som regelsystem har gemensamma mål: att hålla en rättvis och ärlig spel och se till att spelarna får betalt om de vinner. Rättvisa och ärlighet är olika begrepp. En casino kan vara ärlig, men inte rättvist. Ärlighet avser om casino erbjuder spel vars chans element är slumpmässiga. Rättvisa hänvisar till spelet fördel - hur mycket av varje satsad krona bör kasinot att kunna hålla? En slot maskin som håller på i genomsnitt 90% av varje dollar som satsas är verkligen inte rättvist, men kan mycket väl vara ärlig (om utfall av varje spel är inte förutbestämt i casinots fördel). Två viktiga regulatoriska frågor som rör rättvisa och ärlighet - att garantera slumpmässiga resultat och kontrollera husets fördel - är oupplösligt knuten till matematik och mest tillsynsmyndigheterna kräva en viss typ av matematisk analys för att visa spelet fördel och/eller bekräfta att spel resultat är slumpmässiga. Sådana bevis kan vara allt från enkla sannolikhet analyser av datorsimuleringar och komplexa statistiska studier. Kraven varierar mellan olika jurisdiktioner, men det är inte ovanligt att se tekniska språket i spel föreskrifter om särskilda statistiska tester som skall utföras, konfidensintervall som måste uppfyllas, och andra matematiska specifikationer och standarder som gäller för spel resultat.
Sammanfattande tabeller för husets fördel
De två tabellerna nedan visar huset fördelar för många av de populära casino spel. Den första tabellen är en sammanfattning av de populära spelen och den andra ger en mer detaljerad uppdelning.
| Huset fördelar för populära casino spel | om spelet
| husets fördel | | roulette (dubbel-noll) | 5.3% | | craps (pass/come) | 1.4% | | craps (pass/come med dubbla odds) | 0.6% | | blackjack - den genomsnittliga spelaren | 2.0% | | blackjack - 6 däck, grundläggande strategi* | 0.5% | | blackjack single deck, grundläggande strategi* | 0.0% | | baccarat (ingen tie bets) | 1.2% | | caribbean stud* | 5.2% | | let it ride* | 3.5% | | tre kort poker* | 3.4% | | pai gow poker (ante/play)* | 2.5% | | slots | 5% - 10% | | video poker* | 0.5% - 3% | | keno (genomsnitt) | 27.0% | | *optimal strategi |
| Huset fördelar för större kasino insatser | | om spelet | insats | HA* | | baccarat | banken (5% provision) | 1.06% | | baccarat | spelare | 1.24% | | sex stora hjul | genomsnitt | 19.84% | | blackjack | korträkning | -1.00% | | blackjack | grundläggande strategi | 0.50% | | blackjack | genomsnittliga spelaren | 2.00% | | blackjack | dålig spelare | 4.00% | | caribbean stud | ante | 5.22% | | casino war | grundläggande insats | 2.88% | | craps | any craps | 11.11% | | craps | alla sju | 16.67% | | craps | big 6 och big 8 | 9.09% | | craps | köpa (vad som helst) | 4.76% | | craps | C&E | 11.11% | | craps | don 't pass/don' t come | 1.36% | | craps | don 't pass/don' t come-w/1X odds | 0.68% | | craps | don 't pass/don' t come-w/2X odds | 0.45% | | craps | don 't pass/don' t come-w/3X odds | 0.34% | | craps | don 't pass/don' t come-w/5X odds | 0.23% | | craps | don 't pass/don' t come-w/10X odds | 0.12% | | craps | inte plats 4 eller 10 | 3.03% | | craps | inte plats 5 eller 9 | 2.50% | | craps | inte plats 6 eller 8 | 1.82% | | craps | field (2 och 12 år betalar dubbel) | 5.56% | | craps | field (2 eller 12 betalar trippel) | 2.78% | | craps | hard 4 och hard 10 | 11.11% | | craps | hårda 6 och hard 8 | 9.09% | | craps | hop bet - lätt (14-1) | 16.67% | | craps | hop bet - lätt (15-1) | 11.11% | | craps | hop bet - hårt (29-1) | 16.67% | | craps | hop bet - hårt (30-1) | 13.89% | | craps | horn bet (30-1 & 15-1) | 12.50% | | craps | horn hög - någon (29-1 & 14-1) | 16.67% | | craps | horn hög 2, horn hög 12 (30-1 & 15-1) | 12.78% | | craps | horn hög 3, horn hög 11 (30-1 & 15-1) | 12.22% | | craps | lägg 4 eller 10 | 2.44% | | craps | lay 5 eller 9 | 3.23% | | craps | låg 6 eller 8 | 4.00% | | craps | pass/come | 1.41% | | craps | pass/come-w/1X odds | 0.85% | | craps | pass/come-w/2X odds | 0.61% | | craps | pass/come-w/3X odds | 0.47% | | craps | pass/come-w/5X odds | 0.33% | | craps | pass/come-w/10X odds | 0.18% | | craps | plats 4 eller 10 | 6,67 sek% | | craps | plats 5 eller 9 | 4.00% | | craps | plats 6 eller 8 | 1.52% | | craps | tre, elva (14-1) | 16.67% | | craps | tre, elva (15-1) | 11.11% | | craps | två, tolv (29-1) | 16.67% | | craps | två, tolv (30-1) | 13.89% | | keno | typiskt | 27.00% | | let it ride | bas satsning | Med 3,51% | | pai gow | poker duktiga spelare (icke-banker) | 2.54% | | pai gow poker | genomsnittlig spelare (icke-banker) | 2.84% | | röda hund | grundläggande insats (sex kortlekar) | 2.80% | | roulette | enkel nolla | 2.70% | | roulette | dubbel-noll (utom fem-nummer) | 5.26% | | roulette | dubbel-noll-fem-nummer insats | 7.89% | | sic bo | stora/små | 2.78% | | sic bo | en av ett slag | 7.87% | | sic bo | 7, 14 | 9.72% | | sic bo | 8, 13 | 12.50% | | sic bo | 10, 11 | 12.50% | | sic bo | tre av en slag | 13.89% | | sic bo | 5, 16 | 13.89% | | sic bo | 4, 17 | 15.28% | | sic bo | triss | 16.20% | | sic bo | två tärningar kombination | 16.67% | | sic bo | 6, 15 | 16.67% | | sic bo | två av ett slag | 18.52% | | sic bo | 9, 12 | 18.98% | | slots | dollar slots (bra) | 4.00% | | slots | quarter slots (bra) | 5.00% | | slots | dollar slots (genomsnitt) | 6.00% | | slots | quarter slots (genomsnitt) | 8.00% | | sports betting | bet $11 för att vinna $10 | 4.55% | | tre kort poker | pair plus | 2.32% | | tre kort poker | ante | 3.37% | | video poker | utvalda maskiner | -0.50% | | *huset fördelar under typiska förhållanden, uttryckt "per hand" och inklusive band, där så är lämpligt. Optimal strategi antas om inget annat anges. |
Observera: denna sammanfattning är immateriell egendom som tillhör författaren, och university of nevada, las vegas. Inte använda eller reproducera utan ordentlig motivering och tillstånd.
Cabot, anthony N., och hannum, robert C. (2002). Gaming förordning och matematik: Ett äktenskap av nödvändighet, john marshall law review, vol. 35, nr. 3, s. 333-358.
Cabot, anthony N. (1996). Casino spel: politik, ekonomi, och förordning, UNLV international gaming institutet, las vegas, NV.
Eadington, william R., och cornelius, judy (eds.) (1999). Verksamheten av spel: ekonomiska och administrativa frågor, institutet för studier av spel och kommersiella spel, university of nevada, reno, NV.
Eadington, william R., och cornelius, judy (eds.) (1992). Spel och kommersiella spel: uppsatser i företagsekonomi, nationalekonomi, filosofi och vetenskap, institutet för studier av spel och kommersiella spel, university of nevada, reno, NV.
Epstein, richard A. (1995). Teorin om spel och statistisk logik, reviderad upplaga, academic press, san diego, CA.
Fällare, william (1968). En introduktion till sannolikhetslära och dess tillämpningar, 3rd ed., wiley, new york, ny.
Griffin, peter A. (1999). Teorin om blackjack, 6th ed., huntington tryck, las vegas, NV.
Griffin, peter (1991). Extra stuff: gambling svammel, huntington tryck, las vegas, NV.
Hannum, robert C. Och cabot, anthony N. (2001). Praktisk casino matematik, institutet för studier av spel och kommersiella spel, university of nevada, reno.
Ödmjuk, lance, och cooper, carl (1980). Världens största blackjack bok, doubleday, new york, ny.
Kilby, jim och fox, jim (1998). Casino operations management, wiley, new york, ny.
Levinson, horace C. (1963). Slump, tur och statistik, dover publications, mineola, NY.
Millman, martin H. (1983). "En statistisk analys av casino blackjack," american mathematical monthly, 90, s 431-436.
Packel, edward (1981). Matematik spel och gambling, den matematiska association of america, washington, D. C.
Thorp, edward O. (1984). Matematik spel, gambling gånger, hollywood, CA.
Thorp, edward O. (1966). Slå dealern, vintage books, new york, NY.
Vancura, olaf, cornelius, judy A., och eadington, william R. (eds.) (2000). Hitta kanten: matematisk analys av casino spel. Institutet för studier av spel och kommersiella spel, university of nevada, reno, NV.
Vancura, olaf (1996). Smart casino spel, index publishing group, san diego, CA.
Weaver, warren (1982). Lady luck: teorin om sannolikhet, dover publications, new york, ny.
Wilson, allan (1970). Casino gambler ' s guide, harper and row, new york.
Bob hannum är professor i risk analys & spel vid university of denver, där han undervisar på kurser i sannolikhetslära, statistik, risk, och teorin om spel. Hans publikationer kan nämnaspraktisk casino matematik (medförfattare med anthony N. Cabot) och ett flertal artiklar i vetenskapliga och gaming industrin tidskrifter. Hannum regelbundet talar om casino matematik för publik runt om i världen. (del av denna vägledning har hämtats från praktisk casino matematik.)
Följ unlvgaming på twitter och på unlvgamingresearch facebook
© 2019 university of nevada, las vegas. Kopiera inte eller återanvändas utan tillåtelse.
Casino spel matematik
Att spela spel på ett casino – vare sig de är online eller offline – är mycket roligt. Förväntan om en stor vinst, och spänningen i landningen så stor-vinna handen eller spinn, gör spel populär aktivitet som det är. Grundläggande för alla casino spel system av komplexa matematik – många spel som baseras enbart på chans och slumpmässighet, medan vissa spel, såsom blackjack, har även en betydande element av skicklighet. Att förstå matematik casino spel kan hjälpa dig att välja hur du vill placera optimala insatser och ta fram en vettig strategi spel.
Denna del av hemsidan som innehåller information om matematik i olika populära casinospel som roulette, craps, blackjack, poker, keno, bingo och slots. Varje sida handlar om med de viktigaste matematiska principer som gäller för varje enskilt spel, så klicka vidare till din favorit spel nedan för att ta reda på hur de är som styrs av matematik, och hur du kan dra nytta av förståelsen av dessa principer,.
Spel matematik populära kasino spel:
Kom ihåg att den grundläggande matematiken bakom alla casino spel handlar om de principer som i teorin om sannolikhet, som handlar om hur sannolikt eller osannolikt att du finns för att nå ett visst resultat i en given gambling omständighet. Också mycket viktigt att ta hänsyn till när man arbetar ut hur mycket att satsa och när du ska satsa, är om spelet i fråga innebär att oberoende och beroende händelser. Att vara medveten om det förväntade värdet för någon enskild satsning i någon viss casino spel är också en viktig del av en optimal strategi.
Ta reda på mer om matematik spel genom att bläddra på olika sidor på denna webbplats, eller med en snabbt läsa igenom våra spel matematik ordlista om du letar efter en förklaring av ett begrepp relaterade till matematik av casino spel.
Så, låt oss se, vad vi har möjlighet att spela casino spel är en produkt som konsumenten köper med sina spel dollar. Den ståndpunkt som jag tar är att spelaren vill ha en viss erfarenhet när han sitter på ett spel och är villiga att betala för den upplevelsen med hjälp av den oundvikliga bita huset kanten tar. På slot spelet matematiker
| |